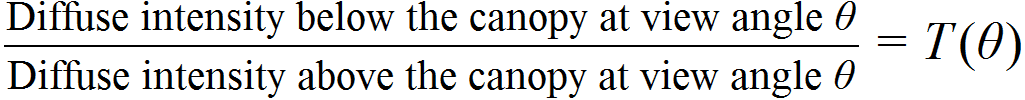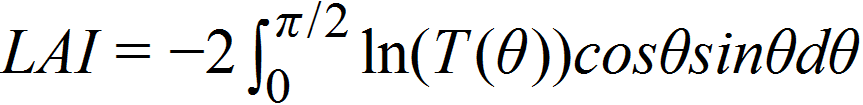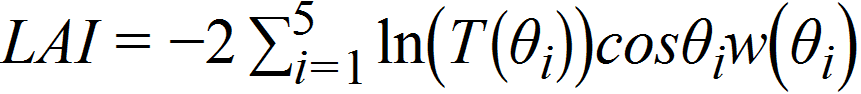Science

测量理论假设

使用LAI-2200C计算叶面积指数（LAI）需要对植被冠层作出一定的假设。这样可以在不破坏性地采样冠层的情况下进行准确测量。LAI-2200C基于以下四个假设进行测量：所有光线都被叶片吸收，叶片分布随机，叶片朝向随机，目标叶片元素(冠层)在传感器视野范围内距离传感器的距离足够远。

没有真正的冠层完全符合这些假设。叶片从不是随机分布的，而是沿着茎和枝干聚集，也不是“黑色的（所有光都被叶片吸收）”。许多物种表现出一定程度的日照性，这违反了方位随机性的假设。然而，许多冠层可以被视为随机分布，活体叶片在490纳米以下具有低透射和反射率。此外，可以通过散射校正纠正由于透射或反射引起的测量误差。

常见的测量误差包括叶片沿着茎秆方向聚集（透射率高于随机模型）。实际上，大多数违反假设的植被，可以通过适当的测量技术来克服，即使没有完全满足所有假设，模型计算结果仍然很好。

所有光线都被叶片吸收

即假设冠层下方的测量值不包括被叶片反射或透射的辐射。注意：在应用散射校正时，此假设将被移除，需在后续数据处理过程中应用叶片反射率和透射率。

叶片随机分布

这些冠层形态可能是：平行状冠层（例如：成行排列的农作物）、单一半球体（例如：孤立灌丛）、无限大箱状体（例如：草原）、带孔无限大箱体（例如：有林窗的落叶林）等。

叶片朝向随机

也就是说，枝叶的倾斜方向不重要，但叶片应该朝向所有方向。

叶片距离传感器镜头要足够远

需确保光学传感器镜头到最近的叶片等元素的距离至少应为叶片宽度的四倍。

计算叶面积指数

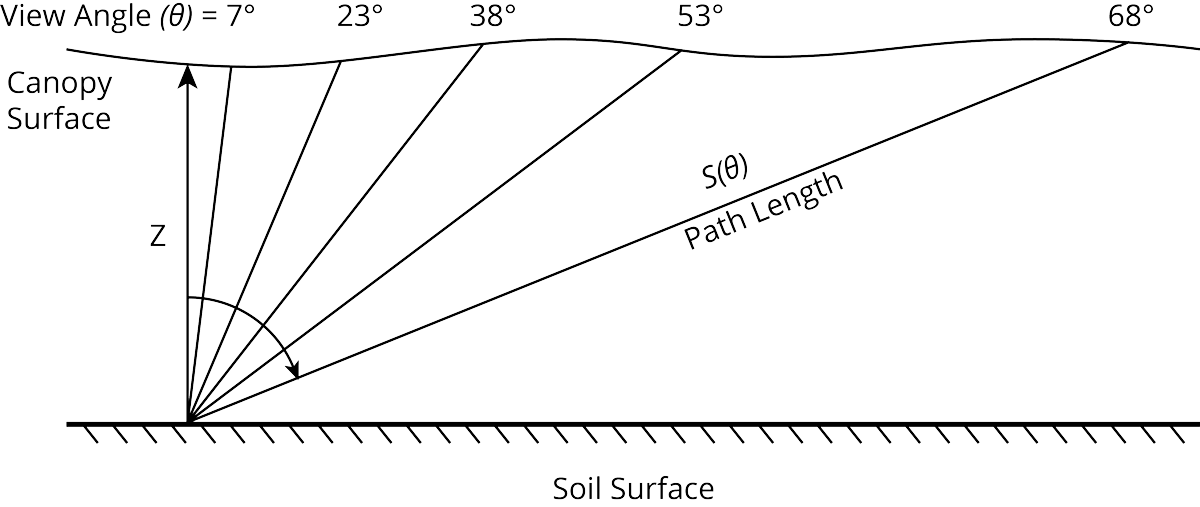
叶面积指数（LAI）是植物单侧叶片面积总和与地面面积的比值。LAI‑2200C从冠层上方和冠层下方进行测量，用于确定5个天顶角度下的冠层光截获。这些数据应用于一个成熟的植物冠层辐射传输模型，计算叶面积指数、平均倾斜角和冠层孔隙度。

LAI‑2200C的光学传感器由一个鱼眼镜头和一个光学系统组成。鱼眼镜头可以“看到”半球形图像，光学系统将其聚焦到光电二极管光学探测器组上，该探测器组由五个同心环状探测器组成。

5 angles for calculating LAI

每个环状探测器对应测量冠层的不同部分，或者说是从天空中心向外延申的5个不同的角度（天顶角）部分。每个天顶角部分穿过植物冠层的漫射辐射分数可以表示为：

equation 1

式中 T(θ) 是给定天顶角（视野环）的漫射非拦截概率，称为孔隙度，类似于透射率。根据比尔-兰伯特定律，T(θ) 取决于叶片朝向、叶片密度和穿过冠层的路径长度，就像光透射通过溶液取决于消光系数、吸收剂浓度和路径长度一样：

equation 2
or
equation 3

式中 ，G(θ) 是朝向视角 θ（天顶角θ ，视野环）投影的叶片比例，μ 是叶片密度（每立方米冠层的叶片面积，类似于浓度），S(θ) 是每个天顶角 θ 的冠层路径长度。米勒（1983）为叶片密度 μ 给出了一个精确解：

equation 4

比值 ln(T(θ))/S(θ) 称为接触数（m-1）。只要 S(θ) 已知，方程2可以应用于任何一般的冠层形状（行、孤立植物等）。对于高度为 z 的全覆盖冠层，S(θ) =z/cosθ；并且 LAI=μ*z，因此方程2可以重写为

equation 5 Soil canopy surface graphic

LAI‑2200C通过使用5个测量的天顶角进行数值积分来实现这个方程。环状探测器几何结构为每个环固定了 sinθdθ 的值，从而可以计算出每个环的常数加权因子 w(θi)。然后数值积分变得非常简单：

equation 6

式中下标 i 指的是第i个环状探测器，该探测器测量的天空部分是以天顶角θi为中心的环。

聚集效应

LAI的计算通常需要进行多次冠层透射率的测量。这些透射率可以在计算LAI之前进行平均，或者更合适的是，在计算冠层LAI之前应该对透射率的对数进行平均，因为这考虑了在传感器视场之外的空间尺度上的聚集效应。LAI‑2200C采用这两种方式计算LAI，但基于后一种方法报告数值。使用这两种方法计算的LAI值的比值被用于估计表观聚集因子（Ryu等，2010；Leblanc等，2005；van Gardingen等，1999；Nilson，1999；以及Nilson和Kuusk，2004）。

叶片朝向

LAI‑2200C根据Lang（1986）的模型计算平均叶倾角（MTA）。也可以使用电脑端软件FV2200C（仪器附带）计算各环的孔隙度等信息。

LAI 2200C Optical Sensor

孔隙度

目前，孔隙度技术是目前间接获取冠层结构参数的一个强大又实用的工具。它不仅适用于连续的冠层，还适用于离散的包含叶片的封闭冠层，如行栽木或孤立木。

可以用孔隙度的测量估算冠层结构信息，包括叶片总量和倾斜角度。

某一冠层的孔隙度，是指冠层下方在某个方向上看到的未被叶片遮挡的视野部分。太阳光斑面积分数等于太阳方向上的孔隙度。

点击下载查看相关文献

散射校正

LAI‑2000和LAI‑2200的传统基本假设之一是，叶片吸收了传感器看到的蓝色波段（320-490纳米）中的所有辐射。这通常是一个良好的假设，适用于漫射光条件，如均质云层的阴天、无云的日出前或日落后的天气。然而，在阳光直射情况下，叶片的反射会导致孔隙度被大大高估，而叶面积指数将被低估。

电脑端软件FV2200在2.0版本允许摒弃这个假设（遵循Kobayashi等人在2013年提出的模型）。它提供了一种模型，用于校正叶片反射和透射辐射对LAI测量造成的影响。在直射阳光下测得的数据应该应用此校正。当有直射阳光存在时，散射误差不可忽略。您也可以在阳光被遮挡时根据实际的叶片散射特性来校正测量结果，而不是假设叶片反射和透射都为零。

散射校正是一项重大改进，特别是需要在冠层下方测量许多值的情况，如异质的森林冠层。现在可以在白天的各个时段进行测量，甚至在晴朗的天空下也可以。非均质阴云或多云天气，尤其是快速移动的云层天气下的测量仍然具有挑战性，但可以通过适当的采样技术进行调整。

散射校正需要的参数：

  • • 太阳位置。LAI-2200C（或配备2200CLEAR升级套件的LAI-2200）可自动提供太阳位置信息。FV2200 软件使用纬度、经度和协调世界时（UTC）来计算太阳天顶角和方位角。
  • 天空辐射特征（由光学传感器测量）
    • 直射光分数。直射光束的总入射辐射分数（蓝色波段）。散射帽覆盖光学传感器镜头测量两个读数，其中一个读数测量时需要被物体遮挡。
    • 天空亮度分布 。需要两种类型的分布：一个用于整个天空，一个用于您用作参考的区域（冠层上方值）。
  • 散射特征。均为蓝光波段的叶片反射和透射以及地面表面反射。

参考文献

  1. Anderson, R. S. 1971. Radiation and crop structure. In: Plant Photosynthetic Production. Manual of Methods. (eds Z. Sestak, J. Catsky, and P. G. Jarvis). W. Junk, The Hague. pp 412-466.
  2. Anderson, R. S., D. R. Jackett, J. L. B. Jupp. 1984a. Linear functionals of the foliage angle distribution as tools to study the structure of plant canopies. Aust. J. Bot. 32: 147-156.
  3. Anderson, R. S., D. R. Jackett, J. L. B. Jupp, J. M. Norman. 1984b. Interpretation of and simple formulas for some key linear functionals of the foliage angle distribution. Agric. and For. Meteor. 36: 165-188.
  4. Bonhomme, R. and Chartier, P. 1972. The interpretation and automatic measurement of hemispherical photographs to obtain sunlit foliage area and gap frequency. Isr. J. Agric. Res. 22: 53-61.
  5. Chen, X. and Campbell, G.S. 1988. Microprocessor controlled instrument for measuring transmitted PAR and sunfleck fraction in plant canopies. Paper presented at American Society of Agronomy, Anaheim.
  6. Kobayashi, H., Ryu Y., Baldocchi, D.B.,Welles, J.M., Norman, J.M. (2013) On the correct estimation of gap fraction: How to remove scattered radiation in gap fraction measurements? Ag. and For. Meteorology, 174-175: 170-183.
  7. Lang, A. R. G., Y. Xiang, and J. M. Norman. 1985. Crop structure and the penetration of direct sunlight. Agric. and For. Meteor. 37: 229-243.
  8. Lang, A. R. G. and Y. Xiang. 1986. Estimation of leaf area index from transmission of direct sunlight in discontinuous canopies. Agric. and For. Meteor. 37: 229-243.
  9. Lang, A. R. G. 1986. Leaf area and average leaf angle from transmittance of direct sunlight. Aust. J. Bot. 34: 349-355.
  10. Lang, A. R. G. 1987. Simplified estimate of leaf area index from transmittance of the sun’s beam. Agric. and For. Meteor. 41: 179-186.
  11. Leblanc, S. G., Chen, J. M., Fernandes, R., Deering, D. W., Conley, A., 2005. Methodology comparison for canopy structure parameters extraction from digital hemispherical photography in boreal forests. Agric. and For. Meteor. 129: 187–207.
  12. Miller, J. B. 1963. An integral equation from phytology. J. Aust. Mat. Soc. 4: 397-402.
  13. Miller, J. B. 1967. A formula for average foliage density. Aust. J. Bot. 15: 141-144.
  1. Nilson, T., 1999. Inversion of gap frequency data in forest stands. Agric. and For. Meteor. 98–99: 437–448.
  2. Nilson, T., and A. Kuusk. 2004. Improved algorithm for estimating canopy indices from gap fraction data in forest canopies. Agric. and For. Meteor. 124: 157–169.
  3. Norman, J. M. and G. S. Campbell. 1989. Canopy structure. In: R. W. Pearcy, J. Ehlringer, H. A. Mooney, and P. W. Rundel (eds) Plant Physiological Ecology: Field Methods and Instrumentation. Chapman and Hall, London and New York, pp 301-325.
  4. Perry, S. G., A. B. Fraser, D. W. Thomson, and J. M. Norman. 1988. Indirect sensing of plant canopy structure with simple radiation measurements. Agric. and For. Meteor. 42: 255-278.
  5. Philip, J. R. 1965. The distribution of foliage density with foliage angle estimated from inclined point quadrat observations. Aust. J. Bot. 13: 357-366.
  6. Ross, J. 1981. The radiation regime and architecture of plant stands. W. Junk. The Hague, 391 pp.
  7. Ryu, Y., T. Nilson, H. Kobayashi, O. Sonnentag, B. E. Law, & D. D. Baldocchi. 2010. On the correct estimation of effective leaf area index: Does it reveal information on clumping effects? Agric. and For. Meteor. 150, 463-472.
  8. Van Gardingen, P. R., Jackson, G. E., Hernandez-Daumas, S., Russell, G., Sharp, L., 1999. Leaf area index estimates obtained for clumped canopies using hemispherical photography. Agric. and For. Meteor. 94 (3–4), 243–257.
  9. Walker, G. K., R. E. Blackshaw, and J. Dekker. 1988. Leaf area and competition for light between plant species using direct sunlight transmission. Weed Technology 2: 159-165
  10. Warren Wilson, J., and J. E. Reeve. 1959. Analysis of the spatial distribution of foliage by two-dimensional point quadrats. New Phytol. 58: 92-101.
  11. Welles, J. M. 1990. Some indirect methods of estimating canopy structure. In: J. Norman and N. Goel (eds) Instrumentation for studying vegetation canopies for remote sensing in optical and thermal infrared regions. Harwood Academic Publishers GmbH, London.
  12. Welles, J. M. and J. M. Norman. 1991. Instrument for indirect measurement of canopy architecture. Agron. J. 83: 818-825.
  13. Welles, J.M. and Cohen, S. 1996. Canopy structure measurement by gap fraction analysis using commercial instrumentation. Journal of Experimental Botany, 47: 1335-1342.

Applications

Continue Reading